超快速可扩展的 Topic 路由 - 第二部分

在我们上一篇博文中，我们讨论了几种 Topic 路由优化方法，并简要介绍了其中两种更重要的方法。在本文中，我们将讨论在实现 DFA 时我们尝试过的一些方法，以及我们对 Trie 和 DFA 进行的一些性能基准测试。

实现 DFA

为了能够构建 DFA，我们首先需要从模式（patterns）构建 NFA。DFA 和 NFA 的主要区别在于，在 DFA 中，在任何一点，您都不需要选择（回溯）；您只需要遵循一条精确的路径遍历图。例如，我们将模式“a.b”和“*.b”转换为 DFA 的方法如下：

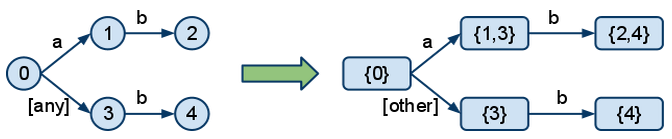
我们可以看到，在 NFA 中，状态 0 有一个选择，如果 Topic 以“a”开头。它可以经过 1 或 3。这会导致回溯。在 DFA 中，对于 Topic 以“a”开头的情况，这两个分支被合并在一起，并将“any”变成了“other”，每种情况只留下一个清晰的选择。

将 NFA 转换为 DFA 有几种选择：

• 使用幂集构造算法。这种方法通常用于从一开始就构造整个 DFA。
• 使用 NFA 算法。这与回溯算法的复杂度相同，但它是通过集合运算来建模的。
• 纯回溯。基本上与上一篇文章中提到的 Trie 方法相同。

转换的主要问题是 DFA 的大小和算法的复杂性。虽然在上面的示例中不明显，但使用模式中的“#”时，DFA 的大小可能会比 NFA 大很多。在某些情况下，“#”会导致一个节点链接到图中的所有其他节点。因此，试图从一开始就构建整个 DFA，然后在每次添加新绑定时完全重建它，将是徒劳的。

为了克服这个问题，我们考虑了一种在创建新模式时修补 DFA 的方法。如何做？构造新模式的 NFA，并像这样将其链接到现有的 DFA：

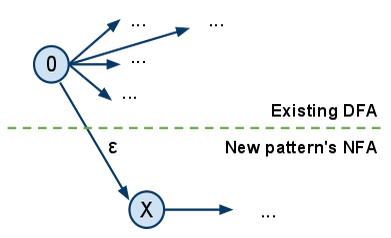
其中 0 是现有 DFA 的起始节点，X 是要添加的新模式的起始节点。

结果将是一个新的 NFA。然后，我们将使用幂集构造方法重建 DFA，但在遇到包含单例集的节点时，如果该元素属于之前的 DFA，我们可以停止并像以前一样链接它。

对于不包含“#”的模式，在大多数情况下，您几乎不会触及现有的 DFA 并完全保留它，同时附加新模式。在这种情况下，添加新绑定的成本会非常低。

问题是……“#”。如果新模式以“#”开头，您将不得不再次遍历整个 DFA 并更新所有节点来重新构造它。因此，并且由于 DFA 的大小复杂度本来就很大，我们最终认为从头开始构建整个 DFA 然后对其进行修补并不是一个好主意。

如今，好的正则表达式编译器不会完全存储 DFA，因为它可能非常庞大。相反，它们会根据需要即时构建 DFA，并使用 NFA 算法进行缓存。您可以将其视为一种惰性求值形式——只有在需要时才会生成新节点。当缓存变得太大时，它们会将其完全丢弃并重新开始。我们在问题中采用了这种方法。

测试 Trie 和 DFA 并尝试改进 DFA

我们编写了一个基准测试来比较两者的性能。我们试图使测试尽可能地模仿 Topic 交换的常见用法。在下文中，“x 倍快”指的是基准测试的时间，通常与朴素实现（不进行上一篇文章中提到的不必要的拆分）相比。基准测试包括将 100 万个 Topic 与 2000 个模式进行匹配。我们在 2.3 GHz 的机器上运行了它。模式包含 0.1 的“*”和 0.01 的“#”。

Trie 在 11.7 秒内完成了我们的基准测试，比朴素实现快了 15 倍。

然后我们对 NFA 算法进行了基准测试，但不缓存 DFA，使用 Erlang 的 digraph 模块来处理图。它的复杂度与 Trie 相当，因此我们预计时间也会相似。结果呢？它非常非常慢！需要数百秒。

我们需要编写自己的图实现，因为 digraph 的性能非常差。因此，我们编写了一个基于 Erlang dict 的专用有限自动机图。仅 NFA（不缓存 DFA）花了 37 秒。比 Trie 慢四倍。仍然不够快。但这可能是因为遍历图而不是树以及执行一些额外的集合运算的成本。

然后我们实现了 DFA 的缓存。结果呢？比 Trie 慢！我们的基准测试结果是 26.7 秒。我们尝试处理更多消息（也许 DFA 没有完全构建）。仍然……更慢。

这是测试的图，当消息数量变化时（2000 个模式，数百万条消息 vs 时间微秒 - 越低越好）：

这相当出乎意料。我们应该在某个时候看到 DFA 以对数方式增长。有什么问题？也许我们需要一个更快的图。众所周知，Erlang 中的 dict 实现速度不快。我们的图实现基于 Erlang 的 dict。我们需要一种方法来优化它。

我们想出了一个动态生成字典源代码的想法。例如，如果您有一个包含条目 `[{k1, v1}, {k2, v2}, {k3, v3}]` 的字典，我们将生成一个函数：

mydict(k1) -> {ok, v1};

mydict(k2) -> {ok, v2};

mydict(k3) -> {ok, v3};

mydict(_) -> error.

因此，它的行为将类似于 dict:find/2 函数，除了它只接受一个参数。我们为此使用了 Yariv Sadan 的 smerl 模块。

我们首先对仅使用 NFA 的新图进行了测试，没有缓存 DFA。在我们的基准测试中，我们获得了 21.9 秒。太棒了！比之前的 37 秒结果快了近一倍。

现在让我们尝试缓存 DFA 并每 5 秒编译一次字典。彻底失败！由于图中的边数非常多，生成的函数有数十万个子句。编译这样的东西需要很长时间！这毫无用处。

仅为 NFA 使用编译后的 dict 而不是缓存的 DFA，我们在基准测试中获得了 15.2 秒——这是我们最快的 DFA 尝试。

进一步测试

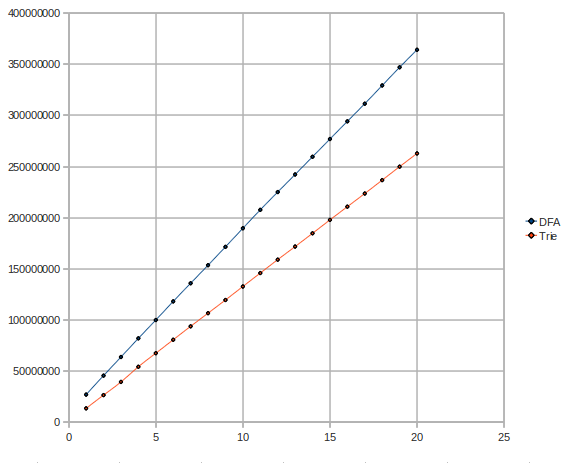
让我们仔细看看 Trie 和 DFA 的复杂度。也许我们可以找到 DFA 出错的原因。这是当模式数量变化时的测试图（300 万条消息，模式数量 vs 时间微秒）：

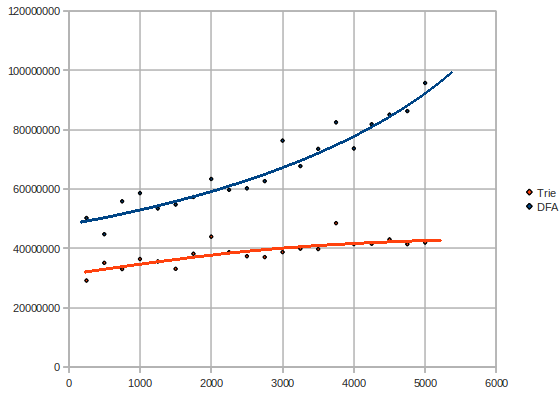
意外！DFA 具有相当指数/二次的复杂度，而 Trie 则保持相当线性或对数复杂度。

可能是什么解释？DFA 使用了很多内存。DFA 慢得多的原因只能是处理器需要非常频繁地从内存中获取 DFA 的部分，而不是能够将 DFA 保存在处理器的缓存中。Trie 使用的内存明显更少，并且可能更适合缓存。

让我们看看内存使用情况，当消息数量变化时（2000 个模式，数百万条消息 vs 使用的字数）：

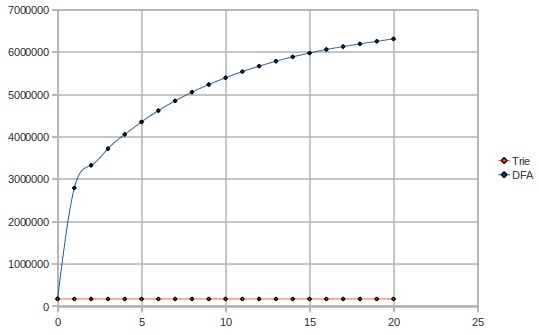
显然，Trie 的大小在消息流动过程中不会改变。我们可以看到，在这种情况下，DFA 使用的内存是 Trie 的 40 倍。事实上，DFA 不适合缓存的理论得到了证实。Trie 使用 1-2MB，而 DFA 使用近 50MB。

现在让我们改变模式的数量并保持消息数量不变（300 万条消息，模式数量 vs 使用的字数）：

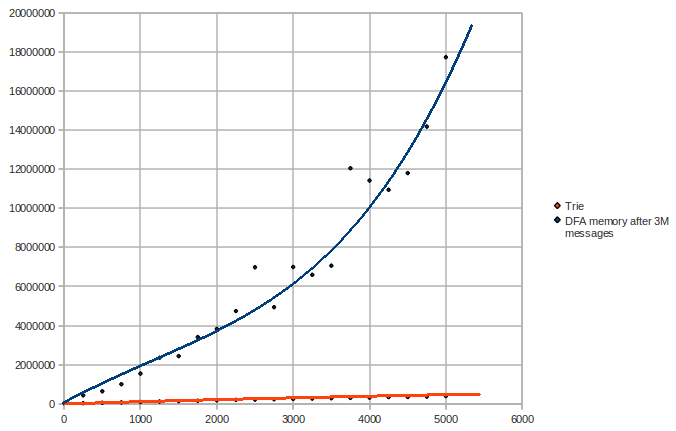
我们在这里可以看到，DFA 具有指数级的空间复杂度。

所以……

缓存消息的 Topic 并按级别索引模式显然不如 Trie 和 DFA 方法。

DFA 使用的内存更多，并且对其进行优化受到许多障碍的限制。即使有专门的图实现，DFA 由于内存使用量大，也无法实现线性时间复杂度，其空间和时间复杂度趋于指数级。这比 Trie 方法明显差，尽管 Trie 会回溯，并且如果每种模式的单词数量在常用情况下更大，它也会具有指数级复杂度。

Trie 方法更简单，因此比 DFA 更易于实现和维护；它使用的内存少得多，因此能够容纳在处理器缓存中；并且在空间和时间上都表现出线性和对数复杂度，使其成为最合适的方法。

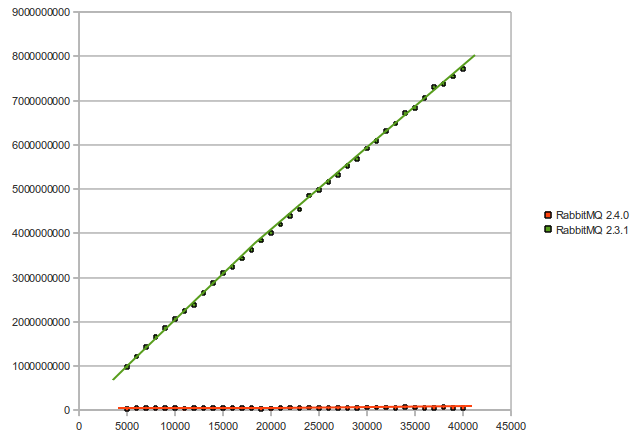
我们在新的 RabbitMQ 版本 2.4.0 中实现了 Trie 方法。这是我们在测试 Rabbit 本身（使用新实现）时得到的结果（绑定的数量 vs 时间微秒）：

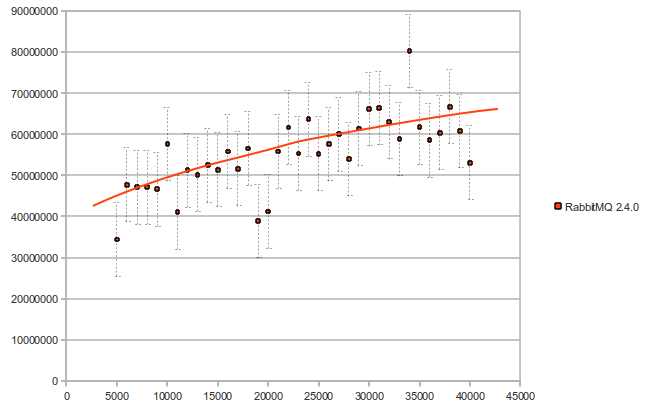
最后，这是版本 2.3.1 和版本 2.4.0 之间的性能比较（绑定的数量 vs 时间微秒）——此图中的性能改进范围为 25 到 145 倍：